アルパカログ

配列の要素から最大値または最小値を得たいとき、要素数がそれほど多くなければ配列をソートしてしまうのが手っ取り早いです。

しかし、要素数が膨大になると配列の全要素のソートはコストが大きくなり、待てども待てども処理が終わらないという少し困ったことになります。特に競技プログラミングやコーディングテストの文脈で、制限時間内に解答が得られなくて困ったりします。

最大値または最小値のみが欲しいとき、この問題は優先度付きキュー（Priority Queue）を使うことで解決することができます。優先度付きキューを実現するにあたっては実装が簡単なヒープがよく利用されるようです。

そこでこの記事では、データ構造の一種であるヒープについて簡単に解説し、ヒープを使った優先度付きキューのJavaScript実装例を紹介します。

ヒープとは、末端ノード以外が二分木でかつ、全てのノードは必ずその子ノードより大きい（もしくは等しい）、または小さい（もしくは等しい）という制約を持つ木構造のことで、前者をMax-Heap、後者をMin-Heapと言います。

Max-HeapとMin-Heap

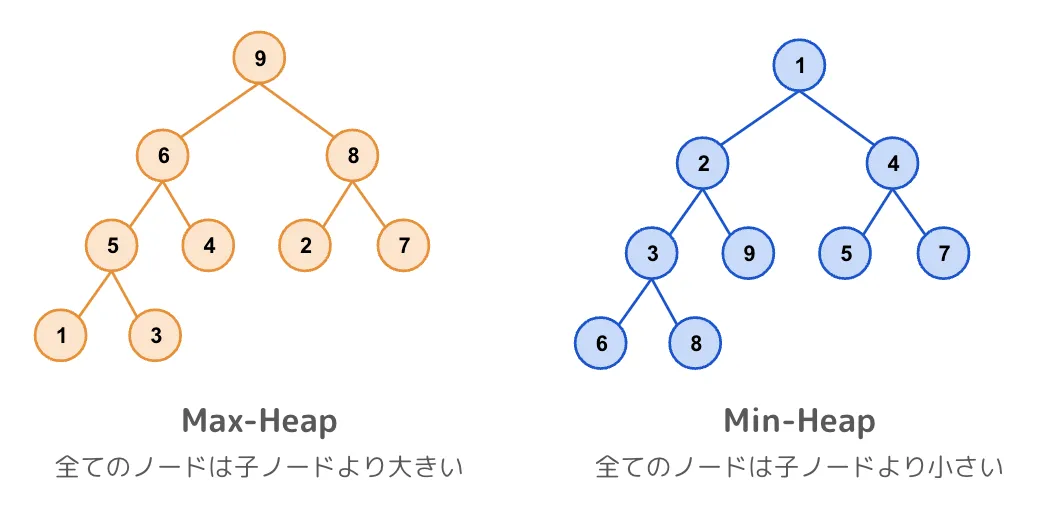
ヒープにおけるルートノードは、Max-Heapでは最大値、Min-Heapでは最小値であることが保証されています。一方、他のノードは位置が保証されていないことに注意が必要です。要素全てを整列するわけではないということは、裏を返すと最大値または最小値を得たいときに効率が良いことを意味しています。

ルートノード以外は位置が保証されていない

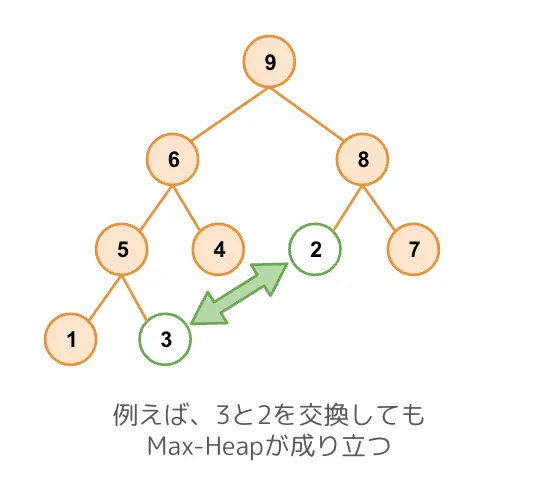
ヒープにおける二分木を配列で表すには、ルートから各階層ごとに左側から右側にかけてノードを配列に格納していきます。したがって配列の先頭要素（i=0）はルートになります。

各階層の左側から順にノードを配列に格納していく

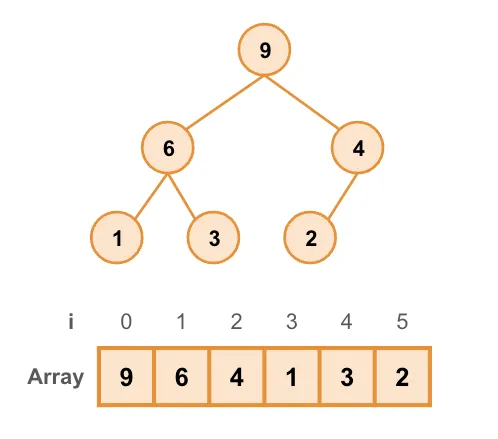
このように配列を作ることで、それぞれのノードのインデックスには次のような関係が成り立ちます。

あるノードのインデックスを i とするとき、その親ノードのインデックス Parent、左側の子ノードのインデックス LeftChild、右側の子ノードのインデックス RightChild は次のようになります。

例えば、図の 6 のノードはインデックス i=1 ですが、その親ノードのインデックスは i=(1-1)/2=0、左側の子ノードは i=1*2+1=3、右側の子ノードは i=1*2+2=4 のように導出することができます。

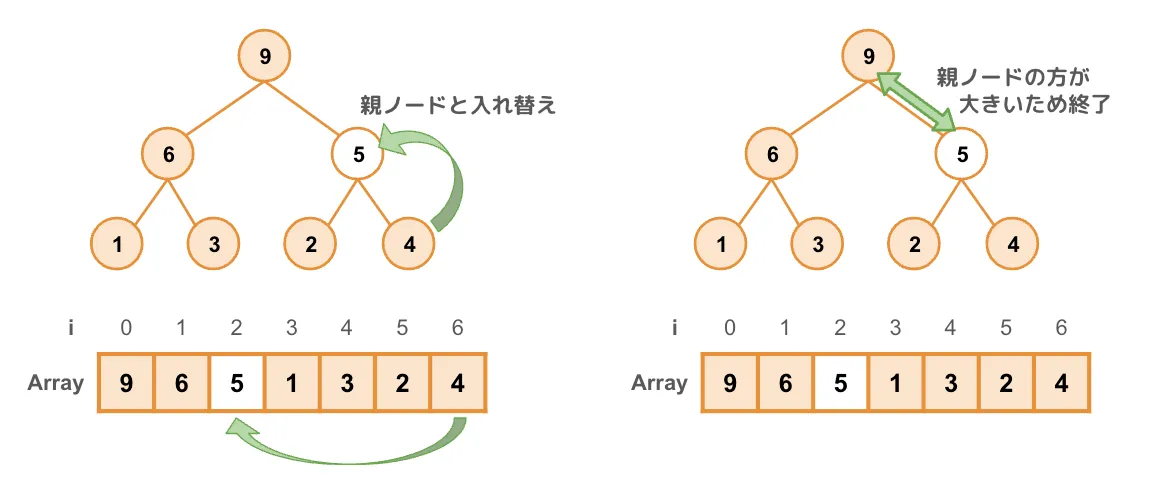
要素の追加をMax-Heapを例に説明します。ヒープに要素を追加するには、まず配列の末尾に要素を追加します。二分木では末端かつ右端のノードにあたります。次に親ノードと比較します。

末尾に追加し親ノードと比較する

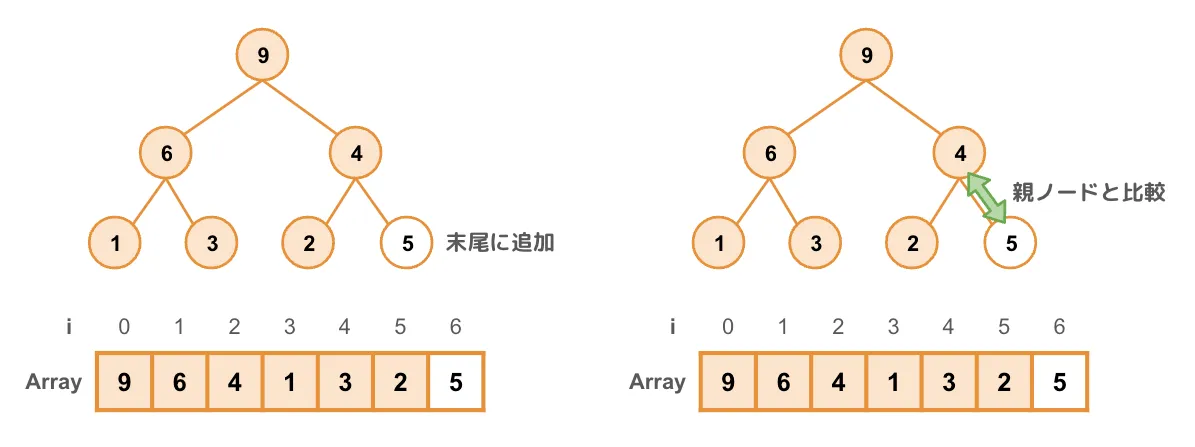
Max-Heapなので、親ノードよりも大きければ入れ替えます。この操作を繰り返ししていき、親ノードの方が大きくなる（もしくは親ノードと等しくなる）か、ルートノードになったら終了します。この操作をSift Up（ふるい上げ）と言います。

親ノードの方が小さければ入れ替え、親ノードの方が大きくなるかルートになるまでこの操作を繰り返す

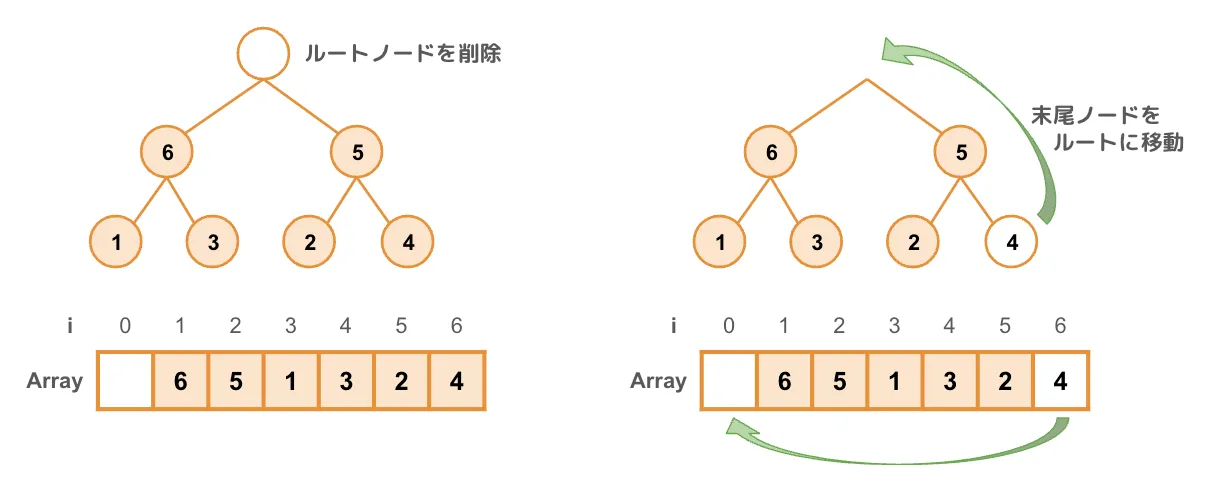
要素の削除もMax-Heapを例に説明します。ヒープからの要素の削除では、ルートノードのみ最大値または最小値が保証されているという特性の利用シーンから、ルートノードの削除を考えます。

ルートノードを削除し、末尾ノードをルートに移動します。

ルートノードを削除したら末尾ノードをルートに移動する

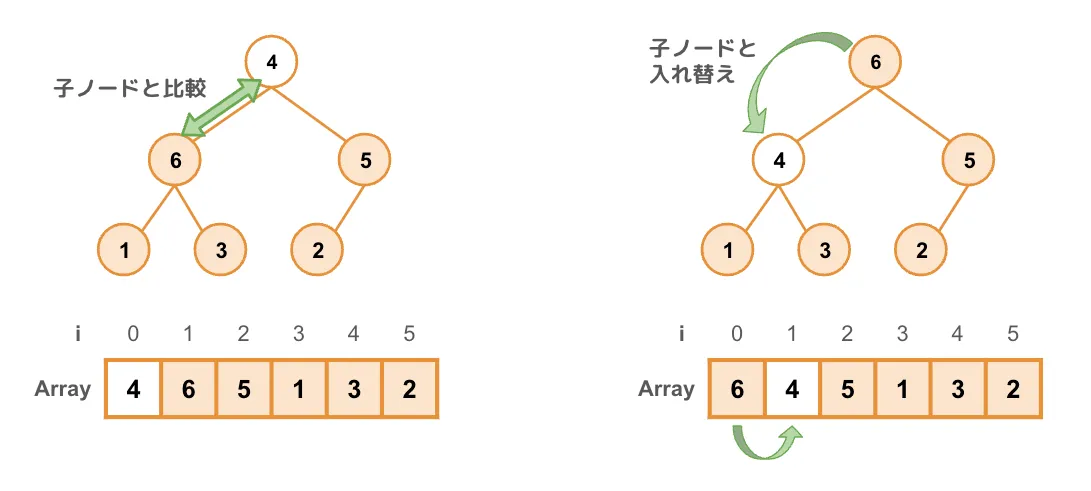
次に、子ノードと比較します。この際、左右の順序には特に制約はありません。比較の結果、子ノードの方が大きければ入れ替えます。

子ノードと比較し、子ノードの方が大きければ入れ替える

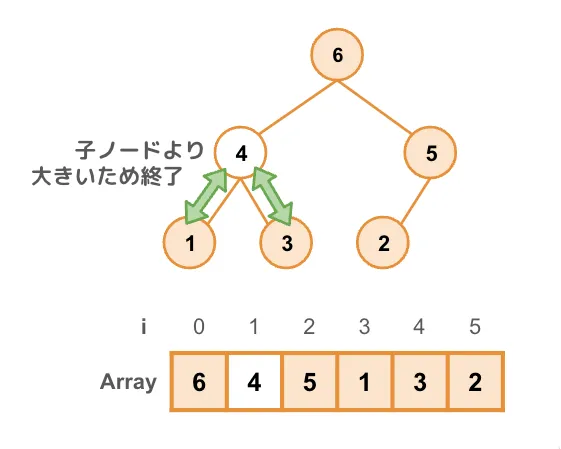
子ノードとの比較、入れ替えの操作を繰り返していき、子ノードの方が小さくなる（もしくは子ノードと等しくなる）か、末端に達したら終了します。この操作をSift Down（ふるい下げ）と言います。

子ノードの方が小さくなるか末端になるまでこの操作を繰り返す

優先度付きキュー（Priority Queue）とは、その名前の通り要素に加えて優先度持つキューで、要素の取り出しでは一番優先度の高い要素を取り除き、返すキューのことを言います。一般的に、配列全体をソートするよりも小さいコストで最大値または最小値を得ることができます。

優先度付きキューはプログラミング言語によっては標準ライブラリでサポートされており、例えばPythonでは heapq で提供されています。

ここでは理解を深めるために、Max-Heapを使った優先度付きキューのJavaScript実装例を紹介します。

class PriorityQueue {
  constructor() {
    this._heap = [];
  }

  push(value, priority) {
    this._heap.push({ value, priority });
    this._siftUp();
  }

  pop() {
    if (this._heap.length === 0) {
      return null;
    }

    const value = this._heap[0].value;
    this._heap[0] = this._heap[this._heap.length - 1];
    this._heap.pop();
    this._siftDown();
    return value;
  }

  size() {
    return this._heap.length;
  }

  _siftUp() {
    let node = this._heap.length - 1;

    while (node > 0) {
      const parent = Math.floor((node - 1) / 2);

      if (this._heap[node].priority > this._heap[parent].priority) {
        [this._heap[node], this._heap[parent]] = [this._heap[parent], this._heap[node]];
        node = parent;
      } else {
        break;
      }
    }
  }

  _siftDown() {
    let node = 0;

    while (node * 2 + 1 < this._heap.length) {
      const left = node * 2 + 1;
      const right = node * 2 + 2;
      let min = left;

      if (right < this._heap.length && this._heap[right].priority > this._heap[left].priority) {
        min = right;
      }

      if (this._heap[node].priority < this._heap[min].priority) {
        [this._heap[node], this._heap[min]] = [this._heap[min], this._heap[node]];
        node = min;
      } else {
        break;
      }
    }
  }
}

下記のようにして使用します。

const queue = new PriorityQueue();
queue.push('A', 1);
queue.push('C', 3);
queue.push('B', 2);

console.log(queue.pop()); // => 'C'

以上です。この記事では、データ構造の一種であるヒープについて簡単に解説し、ヒープを使った優先度付きキューのJavaScript実装例を紹介しました。