Site cover image
Custom icon

アルパカログ
HomeBlog
2025-01-21
Post title iconピックの定理と靴紐の公式およびその利用例
プログラミング

みなさんはピックの定理（Pick's theorem）と靴紐の公式（Shoelace formula、別名：座標法、ガウスの面積公式）をご存知ですか？

おそらく知らない方が多いんじゃないかと思います。特にピックの定理については日本の義務教育では取り扱っていないとのことなので、私も知りませんでした。

ざっくりと言ってしまえば、二つとも座標平面上にある多角形の面積に関する公式で、アプローチの方法が異なります。どちらもプログラムで面積を求めるのに適しており、プログラミングコンテスト（競技プログラミング）で見かけることがあるかもしれません。私はAdvent of Codeという毎年12月に開催されるプログラミングコンテストで存在を知りました。

初めて知ったとき「そんな方法で面積が求められるのか」と目から鱗だったので、知っておいて損はないでしょう。

そこでこの記事では、面積に関する二つの公式「ピックの定理」と「靴紐の公式」とそのユースケースを紹介します。

ピックの定理 靴紐の公式 ユースケース：多角形内部の格子点数を求める

ピックの定理

ピックの定理は、全ての頂点が等間隔の格子点上にあり、穴のない多角形の面積を求める公式で、多角形の内部にある格子点の数を i、辺上にある格子点の数を bとするとき、面積 S は次のように表されます。

S=i+12b−1S = i + \frac{1}{2}b - 1

例として以下のような多角形を考えてみます。

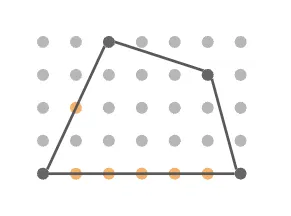
Image in a image block

辺上にある格子点は頂点の4個にオレンジの点6個を加えて10個なので b=10 です。多角形の内部にある点は12個なので i=12 です。よって、面積 S は以下のように求めることができます。

S=12+12⋅10−1=16\begin{aligned} S &= 12 + \frac{1}{2}\cdot10 - 1 \\[2ex] &= 16 \end{aligned}

靴紐の公式

靴紐の公式は別名、座標法、ガウスの面積公式とも呼ばれ、2次元座標平面上の多角形の面積を各頂点の座標から求める公式です。座標さえわかれば面積を求めることができるので、プログラムで面積を求める際に適しています。

各頂点のx座標、y座標を x1, y1, …, xn, yn とするとき、面積 S は次のように表すことができます。

S=12∣∑k=1n(xkyk+1−xk+1yk)∣S = \frac{1}{2}|\sum_{k=1}^n(x_{k} y_{k+1} - x_{k+1}y_{k})|

例として以下のような多角形を考えてみましょう。

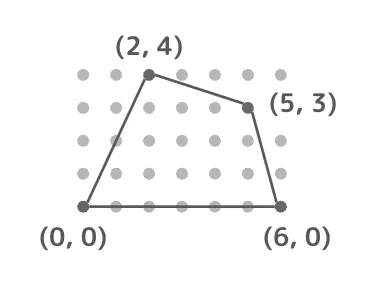
Image in a image block

頂点の座標は左下から時計回りに (x1, y1) = (0, 0), (x2, y2) = (2, 4), (x3, y3) = (5, 3), (x4, y4) = (6, 0) となっています。面積 S は以下のように求めることができます。

S=12∣(0⋅4−2⋅0)+(2⋅3−5⋅4)+(5⋅0−6⋅3)+(6⋅0−0⋅0)∣=12⋅∣−32∣=16\begin{aligned} S &= \frac{1}{2}|(0\cdot4 - 2\cdot0) + (2\cdot3 - 5\cdot4) + (5\cdot0 - 6\cdot3) + (6\cdot0 - 0\cdot0)|\\[3ex] &= \frac{1}{2}\cdot|-32|\\[3ex] &= 16 \end{aligned}

ユースケース：多角形内部の格子点数を求める

ピックの定理と靴紐の公式という二つの方法で多角形の面積が求められることがわかりましたが、どんなときに役立つのでしょうか？

例として、以下のような少し複雑な多角形の内側にある格子点の数を求めることを考えてみます。

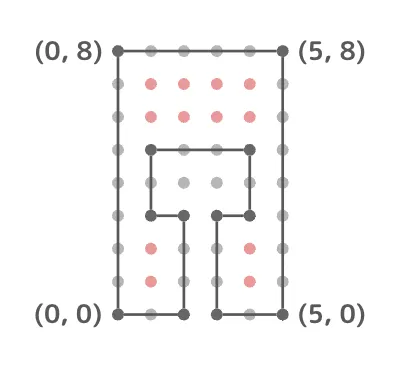
Image in a image block

この程度の複雑さであれば人力で数えることができますが、これをプログラムで解こうとすると結構厄介です。

そこで、ピックの定理と靴紐の公式の出番です。まず、多角形の面積 S を靴紐の公式で求めます。

S=12∣∑k=1n(xkyk+1−xk+1yk)∣S = \frac{1}{2}|\sum_{k=1}^n(x_{k} y_{k+1} - x_{k+1}y_{k})|

靴紐の公式はプログラムのループで以下のように簡単に実現できます。 

const coordinates = [
  {x: 0, y: 0},
  {x: 0, y: 8},
  {x: 5, y: 8},
  {x: 5, y: 0},
  {x: 3, y: 0},
  {x: 3, y: 3},
  {x: 4, y: 3},
  {x: 4, y: 5},
  {x: 1, y: 5},
  {x: 1, y: 3},
  {x: 2, y: 3},
  {x: 2, y: 0},
];

const s = Math.abs(coordinates.reduce((acc, _, i) => {
  const j = (i + 1) % coordinates.length;
  return acc + coordinates[i].x * coordinates[j].y - coordinates[j].x * coordinates[i].y;
}, 0)) / 2;

console.log(s); //=> 31

次に、ピックの定理を多角形内部の格子点数 i を求める式に変形します。

S=i+12b−1i=S−12b+1S = i + \frac{1}{2}b - 1\\[3ex] i = S- \frac{1}{2}b + 1

辺上の頂点数 b は多角形の全ての辺がx軸またはy軸に並行であめ、各頂点の座標から簡単に求めることができます。 

const b = coordinates.reduce((acc, _, i) => {
  const j = (i + 1) % coordinates.length;
  return acc + Math.abs(coordinates[j].x - coordinates[i].x) + Math.abs(coordinates[j].y - coordinates[i].y);
}, 0);

console.log(b); //=> 40

S=31 および b=40 より、多角形内部の格子点数 i は以下のように求めることができます。 

const i = s - b / 2 + 1;
console.log(i); //=> 12

以上です。この記事では、面積に関する二つの公式「ピックの定理」と「靴紐の公式」とそのユースケースを紹介しました。

Thank you!
Thank you!
URLをコピーしました

コメントを送る

コメントはブログオーナーのみ閲覧できます